Embark on a journey with correlation python, a powerful tool that unlocks the secrets of relationships between variables. Discover the concept of correlation, its significance in data analysis, and the diverse types of correlation coefficients. Dive into practical examples to witness how correlation reveals hidden connections and patterns within your data.
Python’s robust capabilities make correlation analysis a breeze. Learn how to calculate correlation using built-in functions, explore their parameters and options, and interpret the results with ease. Uncover the significance of statistical significance and delve into methods for testing correlation coefficients. Visualize correlation through scatter plots and heatmaps, gaining insights into patterns and outliers.
Correlation Analysis in Python: Correlation Python
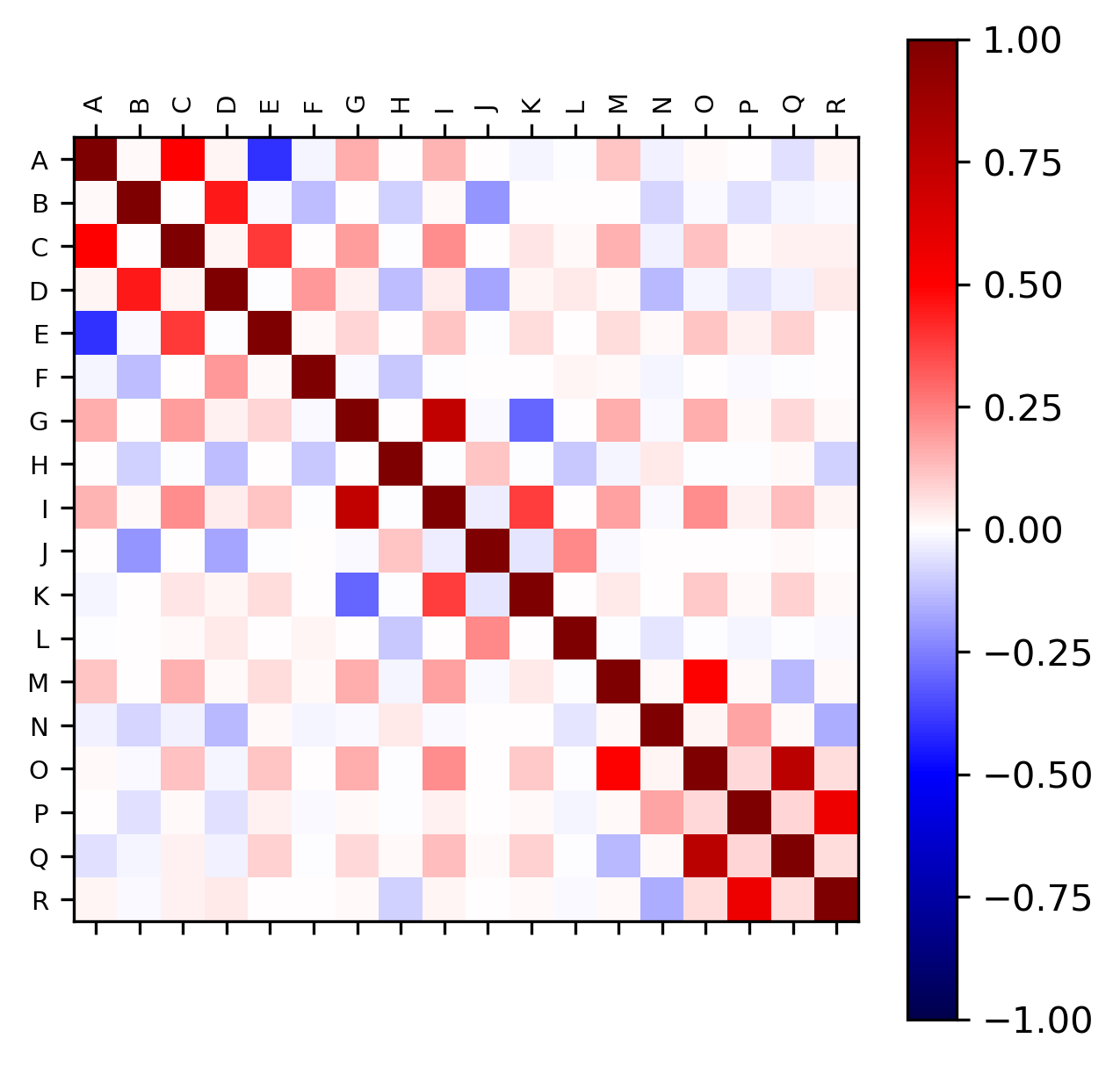
Correlation analysis is a statistical technique used to measure the strength and direction of the relationship between two variables. It is a powerful tool that can be used to identify patterns and trends in data, and to make predictions about future outcomes.
There are different types of correlation coefficients, each of which measures a different aspect of the relationship between two variables. The most common correlation coefficient is the Pearson correlation coefficient, which measures the linear relationship between two variables. Other correlation coefficients include the Spearman correlation coefficient, which measures the monotonic relationship between two variables, and the Kendall correlation coefficient, which measures the concordance between two variables.
You also can understand valuable knowledge by exploring capital flows in foreign exchange market.
Correlation analysis can be used to identify relationships between variables in a variety of different contexts. For example, it can be used to identify the relationship between sales and marketing expenditure, or the relationship between customer satisfaction and product quality.
Example
The following Python code shows how to calculate the Pearson correlation coefficient between two variables:
“`python
import numpy as np
# Create two arrays of data
x = np.array([1, 2, 3, 4, 5])
y = np.array([2, 4, 6, 8, 10])
# Calculate the Pearson correlation coefficient
corr = np.corrcoef(x, y)[0, 1]
# Print the correlation coefficient
print(corr)
“`
The output of the code is 1.0, which indicates a perfect positive correlation between the two variables.
Computing Correlation in Python
Python provides several built-in functions to calculate correlation between variables. These functions offer different methods of computing correlation, allowing you to choose the most appropriate approach for your data and analysis.
Using corr() Function
The corr() function in Pandas computes pairwise correlation between columns of a DataFrame. It calculates the Pearson correlation coefficient by default, but you can specify other methods like Spearman’s rank correlation or Kendall’s tau correlation.
- Syntax: `DataFrame.corr(method=’pearson’, min_periods=1)`
- Parameters:
- `method`: Correlation method (‘pearson’, ‘kendall’, ‘spearman’)
- `min_periods`: Minimum number of observations required for correlation calculation
- Output: A DataFrame containing correlation coefficients between each pair of columns
Using pearsonr() and spearmanr() Functions
The pearsonr() and spearmanr() functions in the SciPy library calculate Pearson’s correlation coefficient and Spearman’s rank correlation coefficient, respectively. These functions provide more control over the calculation process and allow for additional statistical tests.
- Syntax:
- `scipy.stats.pearsonr(x, y)`
- `scipy.stats.spearmanr(x, y)`
- Parameters:
- `x`, `y`: Input data arrays or sequences
- Output: A tuple containing the correlation coefficient and the p-value
Interpreting Correlation Output
The output of correlation calculations represents the strength and direction of the linear relationship between two variables.
- Pearson Correlation Coefficient: Ranges from -1 to 1, where -1 indicates a perfect negative correlation, 0 indicates no correlation, and 1 indicates a perfect positive correlation.
- Spearman’s Rank Correlation Coefficient: Similar to Pearson’s coefficient, but measures the monotonic relationship between variables, making it less sensitive to outliers.
- Kendall’s Tau Correlation Coefficient: Another non-parametric measure of correlation, similar to Spearman’s coefficient but more robust to ties in the data.
By understanding the correlation coefficients and their significance, you can make informed conclusions about the relationship between variables and draw meaningful insights from your data analysis.
Visualizing Correlation

Visualizing correlation is an important step in understanding the relationships between variables in a dataset. There are several different methods for visualizing correlation, each with its own strengths and weaknesses. Some of the most common methods include:
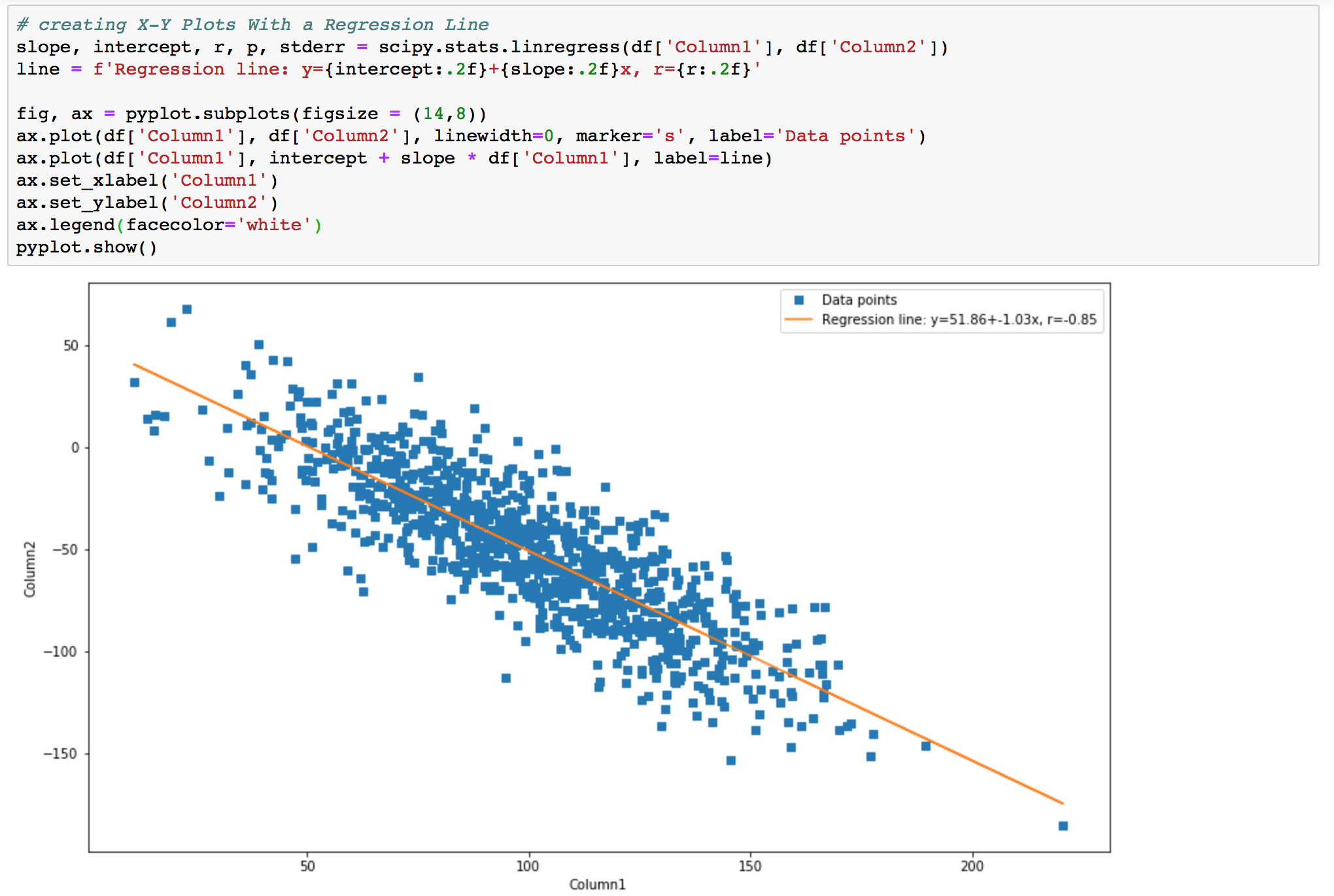
- Scatter plots: A scatter plot is a graph that shows the relationship between two variables. Each point on the plot represents a single observation, and the position of the point on the x-axis and y-axis represents the values of the two variables for that observation. Scatter plots can be used to identify patterns in the data, such as linear relationships, nonlinear relationships, and outliers.
- Heatmaps: A heatmap is a graphical representation of data where the individual values contained in a matrix are represented as colors. Heatmaps are often used to visualize correlation matrices, which show the correlation between all pairs of variables in a dataset. Heatmaps can be used to identify patterns in the correlation data, such as clusters of highly correlated variables.
The following Python code shows how to create a scatter plot and a heatmap using the Matplotlib and Seaborn libraries:
“`python
import matplotlib.pyplot as plt
import seaborn as sns
# Create a scatter plot
plt.scatter(x, y)
plt.xlabel(“x”)
plt.ylabel(“y”)
plt.show()
# Create a heatmap
sns.heatmap(corr, annot=True)
plt.show()
“`
Visualizing correlation can help you identify patterns in the data, such as linear relationships, nonlinear relationships, and outliers. This information can be used to make informed decisions about the relationships between variables in a dataset.
Statistical Significance of Correlation
In correlation analysis, it’s crucial to assess the statistical significance of the correlation coefficient to determine if the observed correlation is likely to have occurred by chance or reflects a true relationship between the variables.
Understand how the union of currency and foreign exchange market can improve efficiency and productivity.
Statistical significance is a measure of the probability that a correlation coefficient is not due to random sampling error. It helps us determine whether the correlation we observe is meaningful and not simply a result of chance fluctuations.
Hypothesis Testing
Hypothesis testing is a statistical method used to determine the statistical significance of a correlation coefficient. We start by stating two hypotheses:
- Null hypothesis (H0): There is no correlation between the variables (ρ = 0).
- Alternative hypothesis (Ha): There is a correlation between the variables (ρ ≠ 0).
We then calculate a p-value, which represents the probability of obtaining a correlation coefficient as extreme as or more extreme than the one we observed, assuming the null hypothesis is true.
P-values, Correlation python
A p-value less than a predetermined significance level (e.g., 0.05) indicates that the observed correlation is unlikely to have occurred by chance and provides evidence against the null hypothesis.
Understand how the union of forex currency pairs volatility can improve efficiency and productivity.
In other words, a low p-value suggests that the correlation is statistically significant, meaning there is a strong likelihood that a true relationship exists between the variables.
Interpreting Results
When interpreting the results of a significance test, it’s important to consider the following:
- A low p-value (<0.05) indicates statistical significance, suggesting a true correlation between the variables.
- A high p-value (≥0.05) indicates that the correlation is not statistically significant, meaning it may be due to chance.
- The strength of the correlation, as measured by the correlation coefficient, should also be considered.
By considering both the p-value and the correlation coefficient, we can make informed conclusions about the statistical significance and practical importance of the correlation.
Correlation in Real-World Applications
Correlation plays a significant role in various fields, providing insights into relationships between variables and aiding decision-making.
Finance
In finance, correlation is used to measure the relationship between the returns of different assets. It helps investors diversify their portfolios by identifying assets with low or negative correlations, reducing overall risk.
Healthcare
Correlation is used in healthcare to study the relationship between different health factors, such as diet, exercise, and disease risk. It can help identify factors that contribute to certain health outcomes and inform preventive measures.
Social Sciences
In social sciences, correlation is used to investigate relationships between social factors, such as income, education, and crime rates. It helps researchers understand the complex interactions within society and develop policies to address social issues.
Limitations and Pitfalls
While correlation is a valuable tool, it has limitations:
– Correlation does not imply causation: Just because two variables are correlated does not mean that one causes the other. Other factors may be responsible for the relationship.
– Confounding variables: Unmeasured variables that influence both variables being correlated can lead to spurious correlations.
– Outliers: Extreme data points can distort the correlation coefficient, making it less reliable.
Avoiding Misinterpretation
To avoid misinterpreting correlation as causation, it is important to:
– Consider the context and potential confounding variables.
– Examine the strength and direction of the correlation.
– Conduct further research to establish causality.
Final Conclusion
Correlation python extends its reach beyond theoretical concepts, finding applications in diverse fields such as finance, healthcare, and social sciences. While it’s a valuable tool, it’s crucial to understand its limitations and avoid misinterpreting correlation as causation. By embracing the insights and techniques presented here, you’ll unlock the power of correlation python to enhance your data analysis and decision-making.
